Pages

Rabu, 08 Februari 2017

Materi 1

Diposting oleh Ananda Ugracena Dharmayoga di 20.04
Hhhaaaiii...
Ini dia materi pertama kami
Materinya adalah tentang ketaksamaan QM-AM-GM-HM
Ketaksamaan AM – GM merupakan ketaksamaan yang paling sering digunakan dalam olimpiade matematika SMA. AM merupakan singkatan dari Arithmetic Means atau rata-rata aritmatika, dan GM merupakan singkatan dari Geometric Means atau rata-rata geometris.
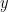Sifat ketaksamaan: AM \geq GM Jika x dan y merupakan bilangan real positif, maka berlaku ketaksamaan:
\frac{x_1 + x_2 + \cdots + x_n}{n} \geq \sqrt[n]{x_1 x_2 \cdots x_n}
Kesamaan didapat saat x_1 = x_2 = \cdots = x_n Ruas kiri merupakan AM dan ruas kanan merupakan GM.
Kesamaan ini didapat dari sifat bahwa kuadrat dari suatu bilangan selalu positif.
Berikut ini bukti ketaksamaan tersebut untuk 2 bilangan, misal p dan q yang keduanya merupakan bilangan real positif.
Karena kuadrat suatu bilangan selalu positif, maka kita dapat:
(\sqrt{p}-\sqrt{q})^2 \geq 0 p-2\sqrt{pq} + q \geq 0 p + q \geq 2\sqrt{pq} \frac{p + q}{2} \geq \sqrt{pq}
Terbukti.
Selain ketaksamaan AM – GM, ada juga sifat ketaksamaan yang lebih luas, yaitu ketaksamaan QM – AM – GM – HM. QM merupakan quadratic means atau rata-rata kuadrat, dan HM merupakan harmonic means atau rata-rata harmonis.
Sifat ketaksamaan: QM \geq AM \geq GM \geq HM \sqrt{\frac{x_1^2 + x_2^2 + \cdots + x_n^2}{n}} \geq \frac{x_1 + x_2 + \cdots + x_n}{n} \geq \sqrt{n}{x_1 x_2 \cdots x_n} \geq \frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + \cdots + \frac{1}{x_n}}
Kesamaan dicapai saat x_1 = x_2 = \cdots = x_n
Untuk contoh soal klik disini

0 komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)