nama kelompok

kelas 7A SMP AMI(Adhi Mekar Indonesia)
ketua: cena
wakil: meylin,dan nicole
tugas: komputer
judul tugas: matholim.blogspot.co.id

rumus kelling lingkaran

Rumus keliling lingkaran - Untuk menghitung keliling dari sebuah lingkaran sama seperti menghitung tepian lingkaran secara penuh.

Keliling = π x d 
Atau karena d = 2 x r , bisa juga di tulis =  π x 2 x jari-jari

d merupakan diameter
r merupakan jari-jari
π = 22/7 atau 3.14

lingkaran dan jari-jarinya

Contoh soal keliling lingkaran

1. Sebuah lingkaran memiliki jari-jari 14 cm. Berapakah keliling lingkaran tersebut?
jawab;

keliling = π x 2 x jari-jari, maka 22/7 x 2 x 14 = 88 cm

2. Berapakan keliling suatu lingkaran yang memiliki diameter  6 m?
jawab :

keliling = π x d , maka 22/7 x 6 = 18,85 m

Baca juga artikel : Rumus luas lingkaran.

3. Jika ada sebuah kolam renang berbentuk lingkaran yang mempunyai diameter 20 m. Jika sesorang berlari mengelilingi kolam tersebut 12 kali, berapakah jarak yang ia tempuh ?
jarak yang ditempuh adalah = 12 x keliling kolam = 12 x 3,14 x 20 = 753,6 m

4. Jika sebuah motor mempunyai roda dengan jari-jari 42 cm berputar sebanyak 2000 kali, berapah jarak yang di tempuh oleh motor tersebut ?

jawab : jarak yang ditempuh motor sama dengan 2000 kali keliling lingkaran ( roda )
maka jarak yang ditempuh motor = 1000 x π x d = 1.000 x 22/7 x 84 cm = 264000 cm = 2,64 km.

5. Sebuah lingkaran mempunyai luas 1256 cm2 hitunglah keliling dari lingkaran itu ?
Luas lingkaran = π r2 ⇔ 1256 = 3,14 x r2
r2 = 1256/3,14 = 400
r = √400 = 20 cm
keliling = 2 π r = 2 . 3,14 . 20 = 125,6 cm

rumus volume tabung dan luas permukaa tabung

Tabung merupakan sebuah bangun ruang tiga dimensi yang memiliki tutup dan alas yang berbentuk lingkaran dengan ukuran yang sama dengan di selimuti oleh persegi panjang.

Tabung

Ciri-ciri tabung

1. Mempunyai dua buah rusuk.
2. Mempunyai alas dan tutup yang berbentuk lingkaran yang sama besar.
3. Memiliki tiga buah sisi yaitu dua buah sisi berbentuk lingkaran dan satu sisi selimut berbentuk persegi panjang.

Rumus Volume Tabung

Untuk menghitung volume sebuah tabung kita bisa menggunakan rumus = Luas alas x tinggi.

Oleh karena itu sebelum menghitung volumenya maka kita harus mengetahui luas alas dari tabung tersebut.

Karena alas tabung berbentuk lingkaran maka rumu luasnya adalah alas tabung = π x r²  ( Lihat disini rumus luas lingkaran )

Nah setelah kita mengetahui rumus alasnya maka kita dapat menggabungkan rumus volume sebuah tabung menjadi

V = π x r² x t

Dimana : V = volume tabung.
                π = phi ( 22/7 atau 3,14 ).
                r  = jari-jari alas.
                t  = tinggi tabung.

Rumus Luas Permukaan Tabung dan Luas Selimut

Luas permukaan merupakan luas dari jumlah sisi-sisi yang di miliki tabung yaitu dua buah alas lingkaran yang sama besar dan satu buah selimut berbentuk persegi panjang.

Rumus luas permukaan tabung  = 2 x π x r x ( t + r )

Rumus luas selimut tabung = 2 x π x r x t 

Dimana :
                π = phi ( 22/7 atau 3,14 ).
                r  = jari-jari alas.
                t  = tinggi tabung.

Rumus tentang luas selimut diatas diperoleh dari = Keliling lingkaran x tinggi tabung. ( lihat rumus keliling lingkaran disini ).

Sedangkan luas permukaan tabung di peroleh dari = dua kali luas lingkaran + luas selimut yang berbentuk persegi panjang.

Setelah melihat pembahasan rumus di atas bagaimana pendapat kamu, Mudah bukan ? Semoga pembahasan tentang rumus volume tabung dan rumus luas permukaan tabung bermanfaat bagi pembaca semua.

Cara Mencari KPK dan FPB

Monday, August 26th 2013. | KPK & FPB

advertisements

KPK dan FPB merupakan salah satu materi yang diajarkan sejak  duduk dibangku SD, apa sampai sekarang materi matematika tersebut masih ada dalam ingatan kita? Bagi yang ingat-ingat lupa, dalam artikel ini akan dijabarkan kembali mengenai KPK dan FPB, dari definisi, cara mencari, serta berbagai contoh soal mengenai KPK dan FPB.

Untuk mencari KPK dan FPB diperlukan hal tentang bilangan prima juga  faktorisasi prima, apa maksud dari kedua ungkapan tersebut :
Bilangan prima merupakan bilangan yang sudah tidak asing lagi yaitu bilangan asli yang hanya mempunyai dua faktor yaitu bilangan itu sendiri dan 1, yang termasuk dalam bilangan prima {2,3,5,7,11,…..}. Sedangkan Faktorisasi prima merupakan penguraian bilangan menjadi perkalian faktor-faktor prima. Untuk melakukan faktorisasi prima ini diperlukan pohon faktor.
contoh:
Faktor prima dari 80 adalah….

buat pohon faktornya:
adversitemens

 

didapat 2 x 2 x 2 x 2 x 5 = 2⁴ x 5
Jadi faktor prima dari 80 adalah 2⁴ x 5

FPB

Faktor Persekutuan Terbesar atau yang familiar disebut sebagai FPB dari dua bilangan merupakan bilangan bulat positif terbesar yang dapat membagi habis kedua bilangan tersebut. Terdapat beberapa metode untuk mencari FPB, yaitu :

1. Menggunakan Faktor Persekutuan

Faktor persekutuan merupakan  faktor yang sama dari dua bilangan atau lebih dan FPB itu sendiri adalah nilai paling besar dari faktor persekutuan dua bilangan atau lebih itu.

Contoh:

carilah  FPB dari 4, 8 dan 12?

Penyelesaian :

Faktor dari 4 adalah = {1, 2, 4}
Faktor dari 8 adalah = {1, 2, 4, 8}
Faktor 12 adalah= {1, 2, 3, 4, 6, 12}
Faktor persekutuannya adalah 1, 2, 4
Nilai yang terbesar adalah 4, sehingga FPBnya adalah 4

2. Menggunakan Faktorisasi Prima

Pada cara ini kita ambil bilangan faktor yang sama, selanjutnya ambil yang terkecil dari 2 atau lebih bilangan.

Contoh:
a. carilah  FPB dari 4, 8 dan 12?
Penyelesaian :
buatlah  pohon faktornya

sehingga faktor dari 4, 8 dan 12 yang sama adalah 2, dan  yang terkecil adalah 2² = 4
Maka FPB dari 4, 8 dan 12 adalah 4
b.Tentukan FPB dari bilangan 20 dan 30

• 2 dan 5 adalah bilangan prima yang sama-sama terdapat faktorisasi prima kedua pohon faktor.
• Pangkat terendah dari 2 adalah 1.
• Pangkat terendah dari 5 adalah 1.
• Maka FPB =  2 X 5  =  10

c.Tentukan FPB dari bilangan 48 dan 60


2 dan 3 merupakan bilangan primayang sama terdapat faktorisasi prima dari kedua pohon faktor, dimana pangkat terendah dari 2 adalah 2 dan pangkat terendah dari 3 adalah 1 sehingga FPB dari kedua bilangan tersebut yaitu 2².3=12
3. Menggunakan Tabel
Cara tabel ini yaitu dengan membagi bilangan yang dicari menggunakan bilangan prima.
contoh :
a. Tentukan FPB dari bilangan 21 dan 35

	21	35
3	7	5
5	7	1
7	1	1

                          FPB  =  3

 b. Tentukan FPB dari bilangan 36 dan 54

	36	54
2	18	27
2	9	27
3	3	9
3	1	3
3	1	1

FPB  = 2 X 3 X 3=  2 X 3²  =  18

Untuk contoh a karena hanya bilangan 3 saja yang bisa membagi habis 21 dan 35 maka FPB = 3

Untuk contoh b hanya yang diberi huruf tebal yang bisa bagi habis bilangan di atasnya saja

c. Tentukan FPB dari bilangan 75, 105 dan 120

	75	105	120
2	75	105	60
2	75	105	30
2	75	105	15
3	25	35	5
5	5	7	1
5	1	7	1
7	1	1	1

                          FPB  =  3  X  5  =  15

KPK

Kelipatan Persekutuan Terkecil atau lebih dikenal dengan sebutan KPK dari dua bilangan merupakan bilangan bulat positif terkecil yang dapat habis dibagi oleh kedua bilangan tersebut. Dalam mencari nilai KPK dari bilangan dapat digunakan beberapa metode, antara lain :

1. Menggunakan Kelipatan Persekutuan

Kelipatan persekutuan merupakan kelipatan yang sama dari dua bilangan atau lebih . KPK adalah nilai terkecil dari kelipatan persekutuan 2 atau lebih bilangan.
Contoh:

carilah  KPK dari 4 dan 8?

Jawab :
Kelipatan 4 adalah = {4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, ….}
Kelipatan 8 adalah = {8, 16, 24. 32. 40, 48, 56, …}Kelipatan persekutuannya adalah 8, 16, 24, 32, …    ( kelipatan yang sama dari 4 dan 8)
Nilai yang terkecil adalah 8, sehingga KPKnya adalah 8

2. Menggunakan Faktorisasi Prima

Hal yang harus dilakukan dalam mencari KPK menggunakan cara faktorisasi prima yaitu mengalikan semua bilangan faktor dan apabila ada yang sama ambil yang terbesar, apabila keduanya sama ambil salah satunya
Contoh:

carilah KPK dari 8, 12 dan 30
Jawab :
buat pohon faktornya

faktor 2 yang terbesar àdalah 2³
faktor 3 nilainya sama untuk 12 dan 30à ambil salah satunya saja yaitu 3
faktor 5 ada 1 à ambil nilai 5
sehingga KPKnya adalah 2³ x 3 x 5 = 120

3. Menggunakan Tabel

Sama hal nya dengan mencari FPB, hakikatnya cara ini memiliki prinsip yang sama

contoh :

a.  Tentukan KPK dari bilangan 16 dan 40

	16	40
2	8	20
2	4	10
2	2	5
2	1	5
5	1	1

                          KPK  =  2 X 2 X 2 X 2 X 5

                                  =   2⁴ X 5  =  80

b. Tentukan KPK dari bilangan 10, 15 dan 25

	10	15	25
2	5	15	25
3	5	5	25
5	1	1	5
5	1	1	1

 KPK  =  2  X 3  X  5  X 5

        =   2 X 3 X 5² =  150

Contoh soal cerita

1.Ali Berenang 10 hari sekali, Budi berenang 15 hari sekali, sedangkan Amir berenang 20 hari sekali. Ketiga-tiganya sama-sama berenang petamakali pada tanggal 20 februari 2012, kapan ketiga-tiganya sama-sama berenang untuk yang keduakalinya?

Jawab:Faktorisasi prima dari 10 = 2 x 5
Faktorisasi prima dari 15 = 3 x 5
Faktorisasi prima dari 20 = 2² x 5KPK dari 10, 15 dan 20 = 2² x 3  x 5 = 60 (kalikan semua faktor, faktor yang sama ambil yang

                                                                     terbesar)
Jadi mereka sama-sama berenang setiap 60 hari sekali.
Mereka sama-sama berenang untuk yang keduakalinya adalah 20 februari + 60 hari = 20 April

Ingat bulan februari untuk tahun kabisat adalah 29 hari, untuk tahun bukan kabisat = 28 hari
(2012 adalah tahun kabisat karena habis dibagi dengan 4)

2. Bu Aminah mempunyai 20 jeruk dan 30 salak, jeruk dan salak akan dimasukkan ke dalam plastik dengan jumlah yang sama.
a. Berapa plastik yang diperlukan?
b. Berapa banyak jeruk dan salak pada masing-masing plastik?Jawab:Faktorisasi prima dari 20 = 2² x 5
Faktorisasi prima dari 30 = 2 x 3 x 5FPB dari 20 dan 30 = 2 x 5 = 10 ( kalikan faktor yang sama, apabila sama ambil yang terkecil)

a. Jumlah plastik yang diperlukan = 10 plastik
b. Jumlah jeruk pada setiap plastik = 20/10 = 2 jeruk
Jujmlah salak pada setiap plastik = 30/10 = 3 salak

3.Pak Andi mendapat giliran ronda setiap 4 hari.  Pak Karim mendapat giliran ronda setiap 6 hari.  Pak Tedi mendapat giliran ronda setiap 8 hari.  Setiap berapa hari mereka ronda bersama-sama ?  Jika mereka ronda bersama-sama tanggal 1 Januari 2008, tanggal berapakah mereka ronda bersama-sama lagi ?

Penyelesaian
KPK dari 4, 6 dan 8

	4	6	8
2	2	3	4
2	1	3	2
2	1	3	1
3	1	1	1

KPK dari 4, 6, dan 8              =  2 X 2 X 2 X 3
=  2³ X 3
=  8  X  3
=  24
Jadi mereka ronda bersama-sama setiap 2

Rumus Volume Kubus

08.47

Rumus Volume Kubus = sisi x sisi x sisi

Dari gambar maka untuk mencari volume kubus adalah

Volume Kubus = AE x AB x AD

Sebelum kita membahas tentang Penjelasan Volume kubus, maka yang harus kita lakukan pertama kali adalah mengenali tentang bangun ruang yang bernama kubus ini. Kubus merupakan salah satu jenis bangun ruang yang memiliki enam sisi dan ke enam sisinya tersebut berbentuk persegi. Kubus memiliki rusuk sebanyak dua belas buah dengan delapan titik sudut. Contoh dari bangun kubus ini dapat kita lihat pada ruangan yang memiliki sisi persegi, pada dadu ataupun benda lain yang memiliki enam sisi berbentuk persegi sama besar. Setelah memahami tentang pengertian dari bangu kubus maka dibawah pada ulasan di bawah kita akan membahas tentang volumenya.

Untuk menghitung volume sebuah kubus maka anda harus memperhatikan hal berikut ini.

- Penjelasan volume kubus: untuk menentukan volume

kubus maka berlaku rumus berikut ini.

V Kubus =
s x s x s atau V Kubus = s3

Keterangan: v = Volume

S = sisi

Contoh soal .

- Pak doni membuat sebuah bak mandi yang berbentuk kubus dengan ukuran sisinya 100 cm. pak doni mengisi bak tersebut dengan air sampai penuh. Maka berapa liter air kah yang diperlukan oleh pak Doni untuk memenuhi bak mandinya?

Jawab :

Diketahui : sebuah bak mandi berbentuk kubus yang memiliki ukuran sisi (s) = 100 cm

Ditanya : Volume kubus?

Jawab: V kubus = s x s x s atau V kubus = s3

V = 100 cm x 100 cm x 100 cm atau V =(100 cm)3

V = 1.000.000 cm3 = 1.000 dm3= 1.000 Liter

Jadi untuk memenuhi bak mandi tersebut maka pak Doni memerlukan air sebanyak 1.000.000 cm3 yang jika kita ubah ke dalam satuan liter menjadi 1.000 liter.

Selain menggunakan cara tersebut misalkan yang diketahui adalah luas persegi salah satu kubus maka yang harus anda lakukan adalah mencari panjang sisinya terlebih dahulu.

Untuk lebih jelasnya anda dapat mengerjakan latihan soal di bawah ini:

- Diketahui sebuah kubus dengan luas salah satu sisinya adalah 100 cm2. maka berapakah volume kubus tersebut?

Dan demikianlah penjelasan volume kubus ini, semoga membantu anda dalam memahami tentang kubus dan yang berkaitan dengan pengukuran volumenya.

rumus gerk sudut beraturan

Gerak lurus beraturan

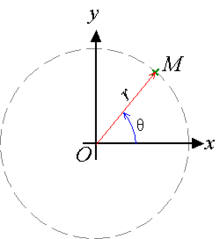
Sistem koordinat kutub dua dimensi

Gerak Lurus Beraturan (GLB) adalah suatu gerak lurus yang mempunyai kecepatan konstan. Maka nilai percepatannya adalah a = 0. Gerakan GLB berbentuk linear dan nilai kecepatannya adalah hasil bagi jarak dengan waktu yang ditempuh.
Rumus:
${\displaystyle \!v={\frac {s}{t}}}$
Dengan ketentuan:

• ${\displaystyle \!s}$ = Jarak yang ditempuh (km, m)
• ${\displaystyle \!v}$ = Kecepatan (km/jam, m/s)
• ${\displaystyle \!t}$ = Waktu tempuh (jam, sekon)

Catatan:

1. Untuk mencari jarak yang ditempuh, rumusnya adalah ${\displaystyle \!s=\!v\times \!t}$.
2. Untuk mencari waktu tempuh, rumusnya adalah ${\displaystyle \!t={\frac {s}{v}}}$.
3. Untuk mencari kecepatan, rumusnya adalah ${\displaystyle \!v={\frac {s}{t}}}$.

Kecepatan rata-rata

Rumus:
${\displaystyle \!v={\frac {s_{total}}{t_{total}}}={\frac {V_{1}\times t_{1}+V_{2}\times t_{2}+...+V_{n}\times t_{n}}{t_{1}+t_{2}+...+t_{n}}}}$

Gerak lurus berubah beraturan

Gerak lurus berubah beraturan adalah gerak yang lintasannya berupa garis lurus dengan kecepatannya yang berubah beraturan.
Percepatannya bernilai konstan/tetap.
Rumus GLBB ada 3, yaitu:

• ${\displaystyle \!v_{t}=\!v_{0}+\!a\times \!t}$

• ${\displaystyle \!s=\!v_{0}\times \!t+{\frac {1}{2}}\times \!a\times \!t^{2}}$

• ${\displaystyle \!v_{t}^{2}=\!v_{0}^{2}+\!2\times \!a\times \!s}$

Dengan ketentuan:

• ${\displaystyle \!v_{0}}$ = Kecepatan awal (m/s)
• ${\displaystyle \!v_{t}}$ = Kecepatan akhir (m/s)
• ${\displaystyle \!a}$ = Percepatan (m/s²)
• ${\displaystyle \!s}$ = Jarak yang ditempuh (m)

Gerak vertikal ke atas

Benda dilemparkan secara vertikal, tegak lurus terhadap bidang horizontal ke atas dengan kecepatan awal tertentu. Arah gerak benda dan arah percepatan gravitasi berlawanan, gerak lurus berubah beraturan diperlambat.
Peluru akan mencapai titik tertinggi apabila V_t sama dengan nol.
${\displaystyle t_{\text{maks}}={\frac {Vo}{g}}}$
${\displaystyle h={\frac {Vo^{2}}{2g}}}$
${\displaystyle t={2}\times {t_{\text{maks}}}}$
${\displaystyle {V_{\text{t}}^{2}}=V_{\text{0}}^{2}-2\times {g}\times {h}}$
Keterangan:

• Kecepatan awal= Vo
• Kecepatan benda di suatu ketinggian tertentu= Vt
• Percepatan /Gravitasi bumi: g
• Tinggi maksimum: h
• Waktu benda mencapai titik tertinggi: t _maks
• Waktu ketika benda kembali ke tanah: t

Gerak jatuh bebas

Benda dikatakan jatuh bebas apabila benda:

• Memiliki ketinggian tertentu (h) dari atas tanah.
• Benda tersebut dijatuhkan tegak lurus bidang horizontal tanpa kecepatan awal.

Selama bergerak ke bawah, benda dipengaruhi oleh percepatan gravitasi bumi (g) dan arah kecepatan/gerak benda searah, merupakan gerak lurus berubah beraturan dipercepat.
${\displaystyle v={\sqrt {2gh}}}$
${\displaystyle t={\sqrt {2h/g}}}$
Keterangan:

• v = kecepatan di permukaan tanah
• g = gravitasi bumi
• h = tinggi dari permukaan tanah
• t = lama benda sampai di tanah

Gerak vertikal ke bawah

Benda dilemparkan tegak lurus bidang horizontal arahnya ke bawah.
Arah percepatan gravitasi dan arah gerak benda searah, merupakan gerak lurus berubah beraturan dipercepat.
${\displaystyle Vt={Vo}+g\times t}$
${\displaystyle Vt^{2}={Vo^{2}}+2\times g\times h}$
Keterangan:

• Vo = kecepatan awal
• Vt = kecepatan pada ketinggian tertentu dari tanah
• g = gravitasi bumi
• h = jarak yang telah ditempuh secara vertikal
• t = waktu

Gerak melingkar

Gerak dengan lintasan berupa lingkaran.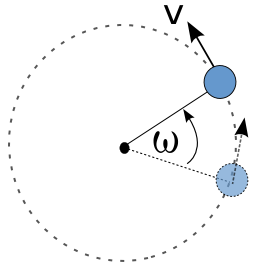

Dari diagram di atas, diketahui benda bergerak sejauh ω° selama ${\displaystyle t}$ sekon, maka benda dikatakan melakukan perpindahan sudut.
Benda melalukan 1 putaran penuh. Besar perpindahan linear adalah ${\displaystyle 2\pi r}$ atau keliling lingkaran. Besar perpindahan sudut dalam 1 putaran penuh adalah ${\displaystyle 2\pi }$ radian atau 360°.
${\displaystyle 2\pi rad=360^{\circ }}$
${\displaystyle 1rad={\frac {360^{\circ }}{2\pi }}={\frac {180^{\circ }}{\pi }}=57,3^{\circ }}$

Perpindahan sudut, kecepatan sudut, dan percepatan sudut

Perpindahan sudut adalah posisi sudut benda yang bergerak secara melingkar dalam selang waktu tertentu.
${\displaystyle \theta =\omega \times t}$
Keterangan:

• ${\displaystyle \theta }$ = perpindahan sudut (rad)
• ${\displaystyle \omega }$ = kecepatan sudut (rad/s)
• t = waktu (sekon)

Kecepatan sudut rata-rata (${\displaystyle {\overline {\omega }}}$): perpindahan sudut per selang waktu.
${\displaystyle {\overline {\omega }}={\frac {\vartriangle \theta }{\vartriangle t}}={\frac {\theta _{2}-\theta _{1}}{t_{2}-t_{1}}}}$
Percepatan sudut rata-rata (${\displaystyle \alpha }$): perubahan kecepatan sudut per selang waktu.
${\displaystyle \alpha ={\frac {\vartriangle \omega }{\vartriangle t}}={\frac {\omega _{2}-\omega _{1}}{t_{2}-t_{1}}}}$
${\displaystyle \alpha }$ : Percepatan sudut (rad/s²)

Percepatan sentripetal

Arah percepatan sentripetal selalu menuju ke pusat lingkaran.
Percepatan sentripetal tidak menambah kecepatan, melainkan hanya untuk mempertahankan benda agar tetap bergerak melingkar.
${\displaystyle A_{s}={\frac {v^{2}}{r}}=\omega ^{2}r}$
Keterangan:

• r : jari-jari benda/lingkaran
• A_s: percepatan sentripetal (rad/s²)

Gerak parabola

Gerak parabola adalah gerak yang membentuk sudut tertentu terhadap bidang horizontal. Pada gerak parabola, gesekan diabaikan, dan gaya yang bekerja hanya gaya berat/percepatan gravitasi.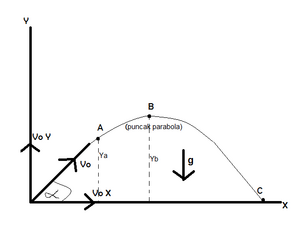

Pada titik awal,
${\displaystyle Vo_{x}=Vo\times \cos \alpha }$
${\displaystyle Vo_{y}=Vo\times \sin \alpha }$
Pada titik A (t = t_a):
${\displaystyle Va_{x}=Vo_{x}=Vo\times \cos \alpha }$
${\displaystyle Va_{y}=Vo_{y}-g\times t_{a}}$
Letak/posisi di A:
${\displaystyle X_{a}=Vo_{x}\times t_{a}}$
${\displaystyle Y_{a}=Vo_{y}\times t_{a}-1/2g{t_{a}^{2}}}$
Titik tertinggi yang bisa dicapai (B):
${\displaystyle h_{max}={\frac {{(Vo\times \sin \alpha })^{2}}{2g}}={\frac {{(Vo^{2}\times \sin ^{2}\alpha })}{2g}}}$
Waktu untuk sampai di titik tertinggi (B) (t_b):
${\displaystyle V_{y}=0}$
${\displaystyle V_{y}=Vo_{y}-gt}$
${\displaystyle 0=Vo\sin \alpha -gt}$
${\displaystyle t_{b}={\frac {{(Vo\times \sin \alpha })}{g}}={\frac {Vo_{y}}{g}}}$
Jarak mendatar/horizontal dari titik awal sampai titik B (Xb):
${\displaystyle X_{b}=Vo_{x}\times t_{b}}$
${\displaystyle X_{b}=Vo\cos \alpha \times ({\frac {{(Vo\times \sin \alpha })}{g}})}$
${\displaystyle X_{b}={\frac {{Vo^{2}}\times \sin 2\alpha }{2g}}}$
Jarak vertikal dari titik awal ke titik B (Yb):
${\displaystyle Y_{b}={\frac {Vo_{y}^{2}}{2g}}}$
${\displaystyle Y_{b}={\frac {{Vo^{2}}\times \sin ^{2}\alpha }{2g}}}$
Waktu untuk sampai di titik C:
${\displaystyle t_{total}={\frac {{(2Vo\times \sin \alpha })}{g}}={\frac {2Vo_{y}}{g}}}$
Jarak dari awal bola bergerak sampai titik C:
${\displaystyle X_{maks}=Vo{x}\times t_{total}}$
${\displaystyle X_{maks}=Vo\times \cos \alpha \times {\frac {{(2Vo\times \sin \alpha })}{g}}}$